Die Assoziativgesetze

Bei der Disjunktion (die Oder-Verknüpfung) und bei der Konjunktion (die Und-Verknüpfung) ist es egal, in welcher Reihenfolge die Aussagen ausgewertet werden. Es gilt:

( A ∨ B ) ∨ C ⇔ A ∨ ( B ∨ C )

bzw.

( A ∧ B ) ∧ C ⇔ A ∧ ( B ∧ C )

 

Hintergrundinfo auf Wikipedia

Verschiedene Schreibweisen sowie neue und alte Schaltbilder für die auf dem LogikBoard verwendeten Gatter sind auf dem folgenden Auszug aus https://de.wikipedia.org/wiki/Logikgatter zusammengefasst.

Wahrheitstabelle:
Assoziativgesetz für ODER-Verknüpfung
A v (B v C) <=> (A v B) v C

A	B	C	B ∨ C	A ∨ (B ∨ C)	A ∨ B	(A ∨ B) ∨ C
False	False	False	False	False	False	False
False	False	True	True	True	False	True
False	True	False	True	True	True	True
False	True	True	True	True	True	True
True	False	False	False	True	True	True
True	False	True	True	True	True	True
True	True	False	True	True	True	True
True	True	True	True	True	True	True

 

Schaltung am LogikBoard: Assoziativgesetz für ODER-Verknüpfung A v (B v C) <=> (A v B) v C

linke Seite	rechte Seite

 

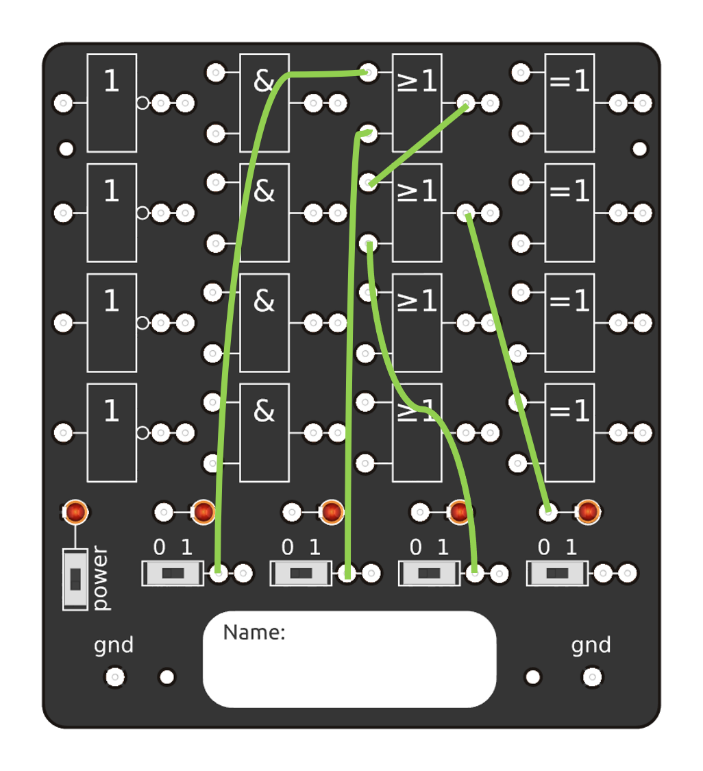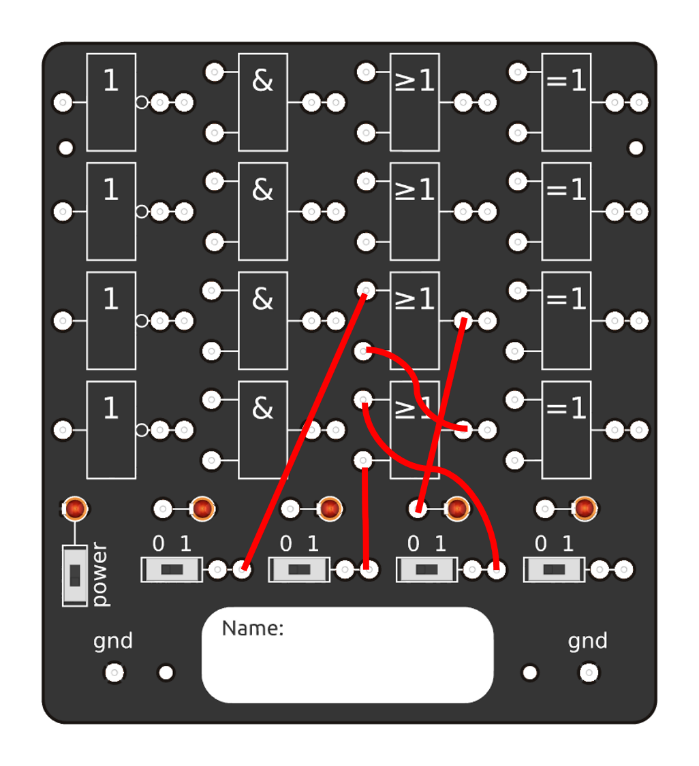Die drei linken Schiebeschalter simulieren die Eingangsgrößen A, B und C. Es gibt acht verschiedene Möglichkeiten für die Schalterstellungen: 0-0-0, 0-0-1, 0-1-0, 0-1-1, 1-0-0, 1-0-1, 1-1-0 und 1-1-1.
Zu jedem Zeitpunkt müssen die beiden rechten LEDs, die die Ausgangsgrößen der zwei Schaltungen zeigen, gleichermaßen AN oder AUS sein.

Übungsaufgabe: Zeige die Gültigkeit des Assoziativgesetzes für UND-Verknüpfungen